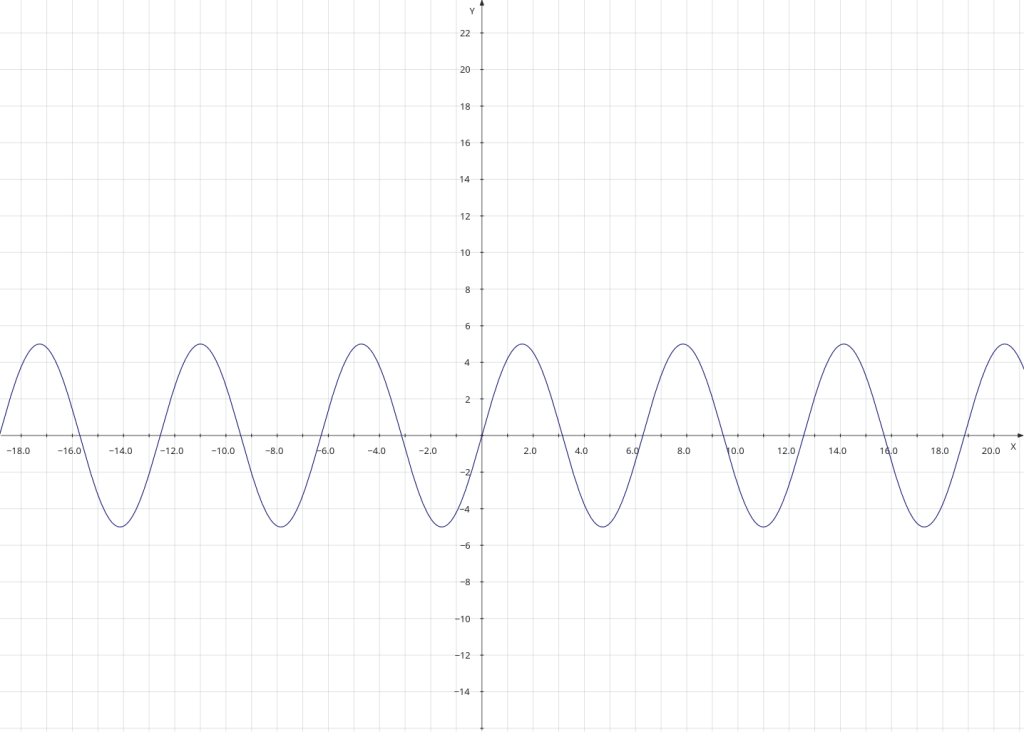
A simple sine wave is not that interesting. However adding sine waves together can produce something more aesthetically satisfying. I could, for example, add another sine wave with a higher frequency to the above simple sine wave, as shown below.
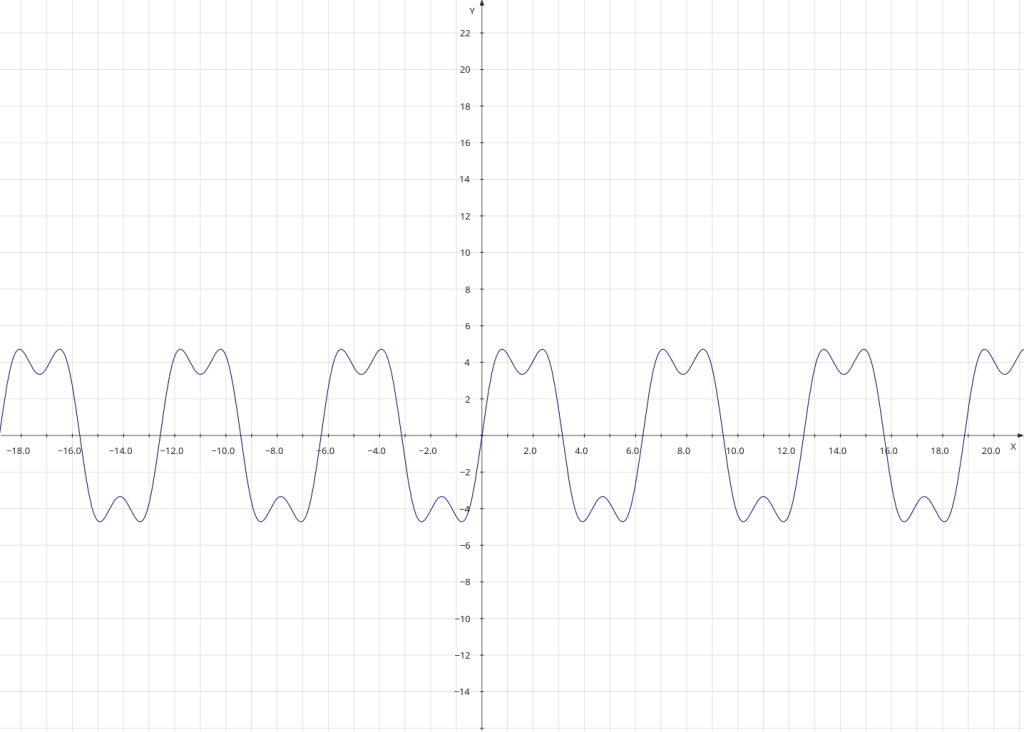
The above diagram shows the result of adding a sine wave of three times the original frequency to the first wave. Below I show the result of adding a third sine wave of five times the original fequency to the first.
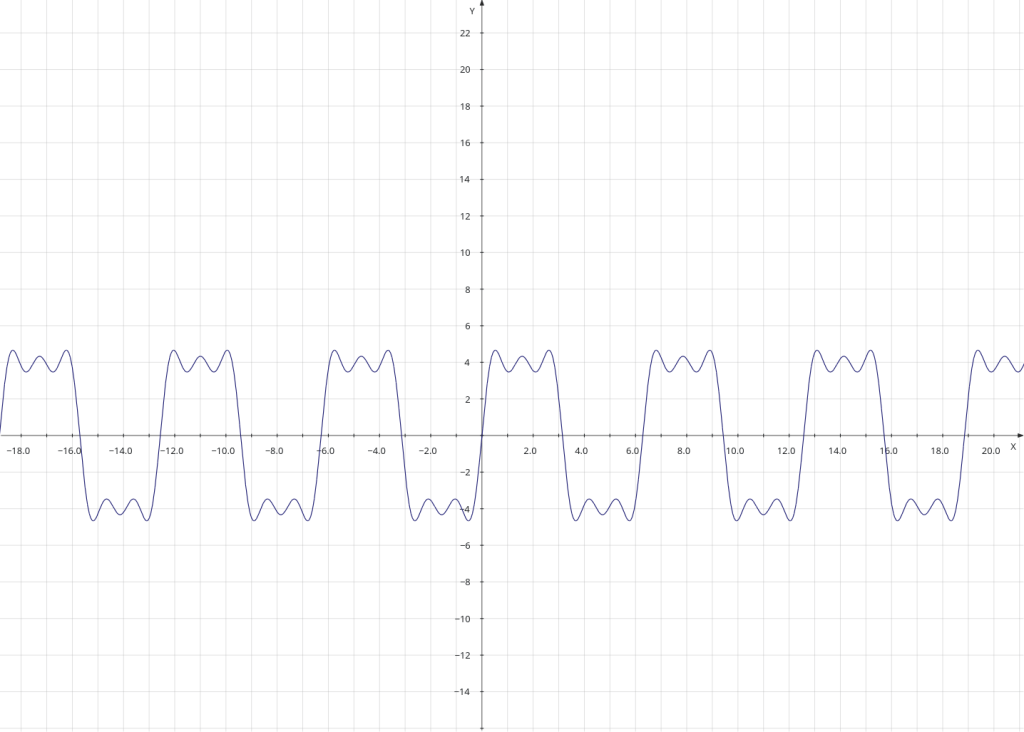
A pattern is beginning to emerge from this process. I’ll add a few more terms to the summation.
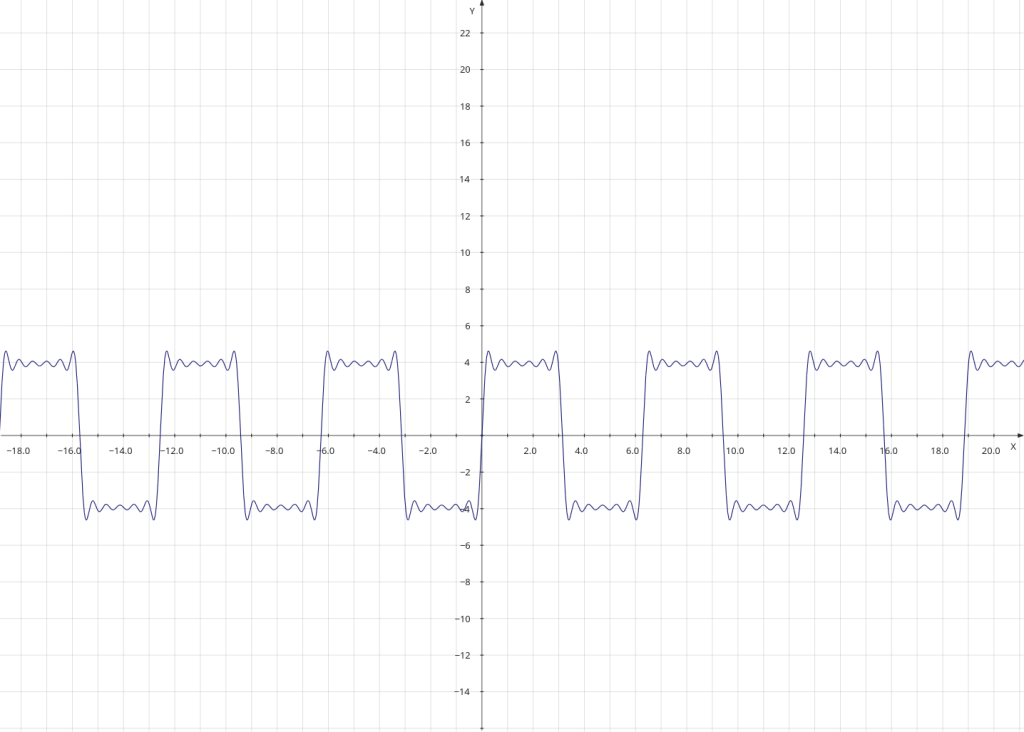
This shows the sum of the terms up to the the term for the sine wave which is 13 times the original frequency. Those who have done some maths probably recognise that this is tending towards a square wave. Here’s a link to a MatLab version of what I’ve done here.
Here’s a depiction of all the individual waves that have been added together, plus the final result.

Here’s an image of just a few of the waves. It’s probably more aesthetic than the full set!
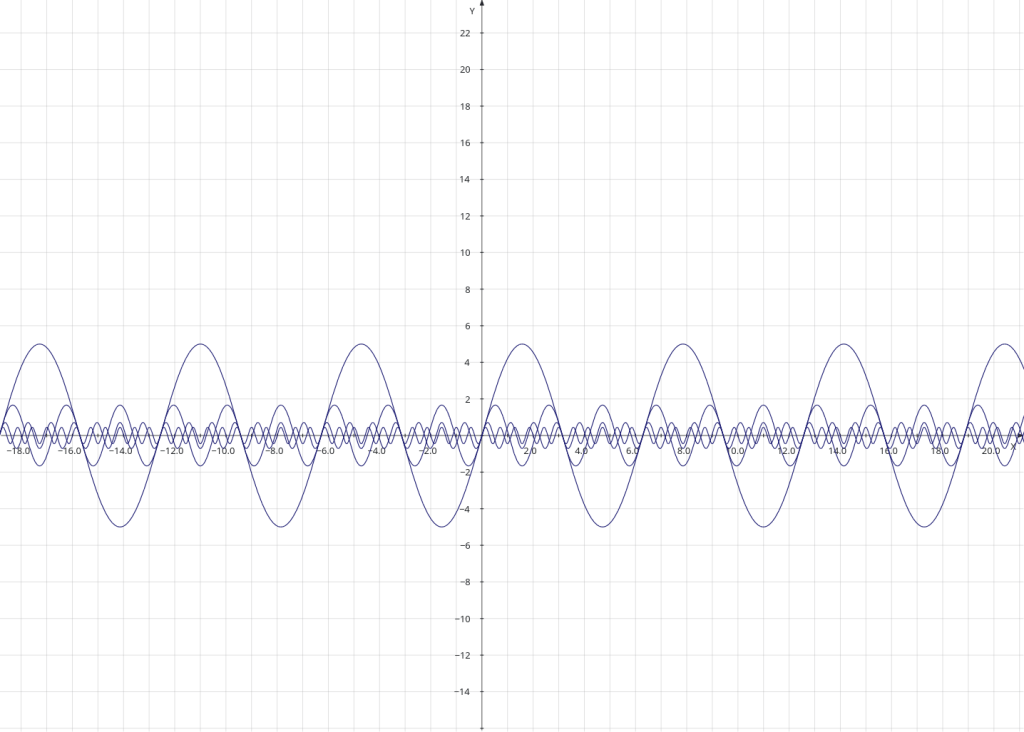
A couple of times when I was creating the above series of plots, I made mistakes, and ended up with some more interesting graphs, but I discarded those ‘mistakes’ and stuck closely to my original idea, which was to show how simply adding a few sine waves together could result in an approximate square wave.
In fact the Fourier series for a square wave can be expressed as an infinite sum of sine waves, as shown here. A fairly complex mathematical fact can be approximated by a few simple plots.
Now I’m going to go back to the ‘mistakes’ that I made and rejected earlier when developing and writing this post.
