‘Spirograph’ includes toothed rings which can be used with small disks to draw Spirograph patterns inside the ring. The small toothed rolls around the inside of the fixed ring, producing the typical Spirograph spirals.
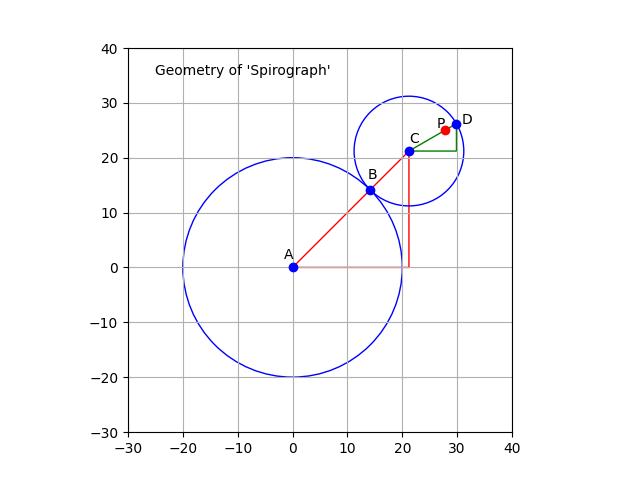
The diagram above shows how this works. The small circle rolls around inside the larger circle (which represents the inside of the ring). If there is no slippage, the small circle rotates in the opposite direction to its movement around the larger circle.
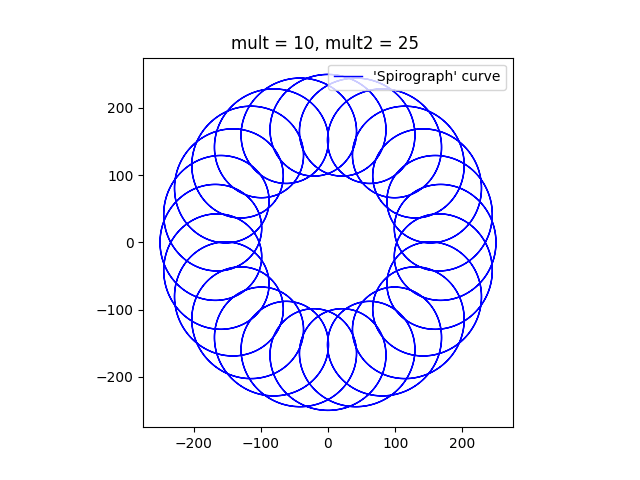
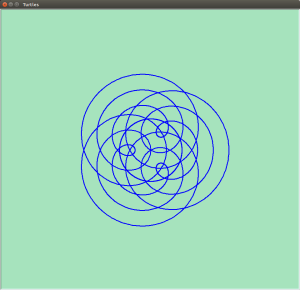
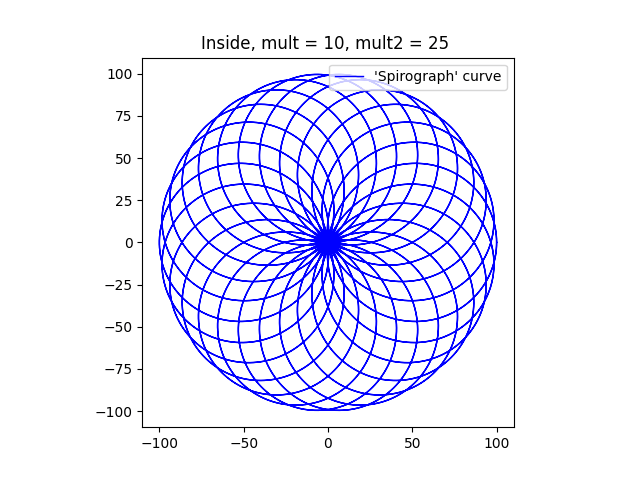
I modified my Python program to simulate this situation. As before, the rate of rotation of the smaller circle can be controlled by varying the ‘mult2’ variable in the program. To start with I used a small value for the variable as shown below.

The diagram has five ‘lobes’ and an empty patch in the middle. The curve can never go through the centre. If the ratio of the sizes of the circles is less than one half, then smaller circle is not big enough to reach the centre of the larger circle. If the ratio of the sizes of the circles is greater than one half, then the point on the circumference of the smaller circle that is drawing the curve (point D on the diagram above) never falls on the centre of the larger circle. If the ratio of sizes is exactly one half, all the loops will pass through the centre of the larger circle.
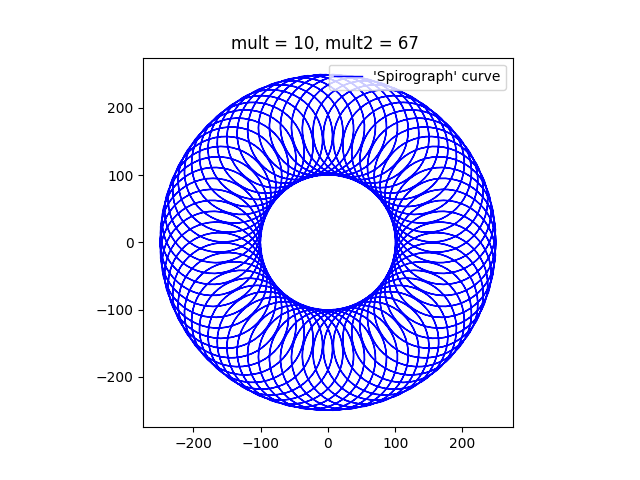
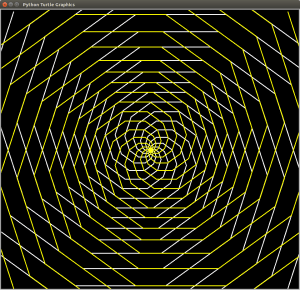
As the multiplier ‘mult2’ is increased, the curve comes to resemble the circular shape of a typical Spirograph. I think that it looks a bit like a torus or a donut.

I’m not going to try to emulate the behaviour of the non-circular Spirograph components. In fact, I have only emulated the circular ones, but not completely. I’ve only plotted the curves that would result if the point P (the pen) corresponded to the point D (on the smaller circle) in the diagram above.
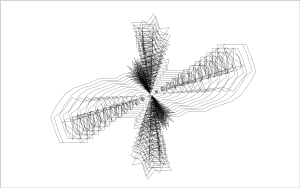
Here’s one final plot, where the ratio of the smaller circle to the larger circle is exactly one half. The program draws a pleasant chrysanthemum or dahlia shape.
Finally, here’s the Python program that I used to draw these diagrams. To get the different figures, I’ve changed the multipliers, mainly ‘mult2’. I’ve also changed the sizes of the circles (variables ‘large’ and ‘small’) to get some of them.
import numpy as np
import matplotlib.pyplot as plt
# Dimensions of two circles
r1 = 100
r2 = 50
# c0 = [0,0]
# c1 = [1,0]
# Multipliers
mult = 10 # Used to generate the number of points plotted.
mult2 = 25 # Controls speed of rotation of the smaller circle, relative to the first.
ax = plt.subplot()
ax.set_aspect( 1 )
# Parametric array for the larger circle
t1 = np.linspace(-2 * np.pi, 2 * np.pi, mult * 360)
# Parametric array for the smaller circle
t2 = t1 * mult2
# Calculation of X/y cordinates using the parametric arrays.
# x0 and y0 are the coordinates of the tangential point, B.
x0 = r1 * np.cos(t1)
y0 = r1 * np.sin(t1)
# plt.plot(x0, y0, label=("Large circle"), color = 'r', linewidth = 2, linestyle = '--')
# x1 and y1 are the cordinates of the centre of the small circle, C.
x1 = (r1 - r2) * np.cos(t1)
y1 = (r1 - r2) * np.sin(t1)
# x1a and y1a are the coordinates of D relative to C.
x1a = r2 * np.cos(t2)
y1a = r2 * np.sin(t2)
# plt.plot(x1a, y1a, label=("Small circle"), c = 'r', linewidth = 2, linestyle = '--')
# x2 and y2 are the coordinates of the desired point on the curve, D.
plt.plot(x0[0],y0[0], color='r')
# The small circle rolls in the opposite direction if it is inside
x2 = r2 * np.cos(-t2)
y2 = r2 * np.sin(-t2)
# Plot the Curve
# plt.plot(x1 - 1.5 * x2, y1 - 1.5 * y2)
plt.plot(x1 + x2, y1 + y2, label=("'Spirograph' curve"), c = 'b', linewidth = 1)
plt.title("Inside, mult = {}, mult2 = {} ".format(mult, mult2))
plt.legend(loc="upper right")
plt.show()